Informationen zum Praktikumsteil 3
für den Bachelorstudiengang Physik und für Lehramt an Beruflichen Schulen
Termine Teil 3
-
Anmeldetermine
Die Anmeldung zum Praktikumsteil 3 ist vom 16.01.2023 bis 05.02.2023 (Blockpraktikum) bzw. vom 27.03.2023 bis 10.04.2023 (Semesterpraktikum).
-
Blockpraktikum im März 2023 und Semesterpraktikum SoSe 2023
| Block A | Block B | Semester | ||
|---|---|---|---|---|
| Kurs 1: 9:00-13:00 Uhr | Kurs 3: 9:00-13:00 Uhr | Kurs 5: Mo., 14:15-17:15 Uhr | ||
| Kurs 2: 14:00-18:00 Uhr | Kurs 4: 14:00-18:00 Uhr | |||
| 1. Termin | 06.03.23 | 07.03.23 | 24.04.23 | |
| 2. Termin | 08.03.23 | 09.03.23 | ||
| 3. Termin | 10.03.23 | 13.03.23 | ||
| 4. Termin | 14.03.23 | 15.03.23 | ||
| 5. Termin | 16.03.23 | 17.03.23 | ||
| 6. Termin | 20.03.23 | 21.03.23 | ||
Stand: 04.11.22
Anmeldung zu Teil 3
- Der Anmeldezeitraum für den Praktikumsteil 3 ist vom 16. Januar 2023 bis zum 05. Februar 2022 (Blockpraktikum).
- Die Anmeldung läuft über die Lehrveranstaltungsanmeldung in TUMonline. Sie gelangen dorthin entweder über Ihren CurriculumSupport (Studienbaum) oder über die Lehrveranstaltungssuche.
- Die Platzvergabe erfolgt nicht nach Anmeldezeitpunkt. Kriterien sind die Zuordnung des Praktikums zum Studienplan, die biher absolvierten Credits im Studium und das Fachsemester.
- Zur Teambildung können Sie bei der Anmeldung einen Teamnamen vergeben. Dieser darf bei Maximal zwei Anmeldungen vorkommen, die dann zu einer Teananmeldung zusammengefasst werden.
- Sie können bei der Anmeldung die für Sie infrage kommenden Wochentermine auswählen, und dabei eine Priorisierung vornehmen.
https://www.tum.de/die-tum/aktuelles/coronavirus/praxisveranstaltungen/
teilnehmen werden.
Die Teilnahme am Praktikum ist ausgeschlossen, wenn Sie nach der geltenden Einreise-Quarantäneverordnung unter Quarantäne stehen, Sie Kontakt zu einem COVID-19-Erkrankten hatten oder am Praktikumstag Symptome haben.
Personen, die einer Gruppe mit erhöhtem Risiko für einen schweren Verlauf angehören und an dem Praktikum teilnehmen möchten, sind gehalten, die notwendigen Maßnahmen zum Eigenschutz zu treffen bzw. von einer Teilnahme abzusehen. Hier kann der Krisenstab (krisenstab-coronavirus@tum.de) oder der behandelnde Arzt beraten.
-
Kontakt für weitere Fragen: Dr. Martin Saß
Versuchesreihenfolge in Teil 3
Ihre individuellen Termine und die Versuchsreihenfolge finden Sie im zugeordneten Moodle-Kurs.
Versuche im Teil 3
Versuch: Franck-Hertz-Versuch (FHV)
-
Kurzbeschreibung
-
Downloads
Anleitung FHV
Anleitung FHV (ältere, englische Version) -
Versuchsaufbau
 Abbildung 1: Überblick über den Versuchsaufbau mit der Hg-Röhre
Abbildung 1: Überblick über den Versuchsaufbau mit der Hg-Röhre
 Abbildung 2: Der Franck-Hertz-Versuch mit Noen
Abbildung 2: Der Franck-Hertz-Versuch mit Noen
Reicht die Energie der Elektronen aus, um Ne-Atome anzuregen, entsteht eine Schicht angeregter Atome am Anodengitter. Beim (mehrstufigen) Übergang der Atome in den Grundzustand wird auch Licht im sichtbaren Bereich ausgesendet, so dass eine leuchtende Schicht sichtbar wird. Bei Erhöhung der Beschleunigungsspannung wandert diese Schicht zur Kathode hin. Reicht die Energie aus, dass eine weitere Anregung möglich ist, entsteht eine weitere Leuchtschicht an der Anode.
Versuch: Radioaktivität (RAD)
-
Kurzbeschreibung
In diesem Versuch werden γ-Spektren verschiedener radioaktiver Präperate aufgenommen und ausgewertet.
-
Downloads
- Anleitung RAD
- Das beim Versuch verwendete Messprogramm Cassy Lab kann bei Bedarf als Demoversion mit 20 freien Aufrufen von der Internetseite der Firma LD Didactic GmbH heruntergeladen werden.
- Rechtlicher Hintergrund:Strahlenschutzgesetz und Strahlenschutzverordnung
(auch verfügbar über das Portal Umwelt Online)
-
Versuchsaufbau
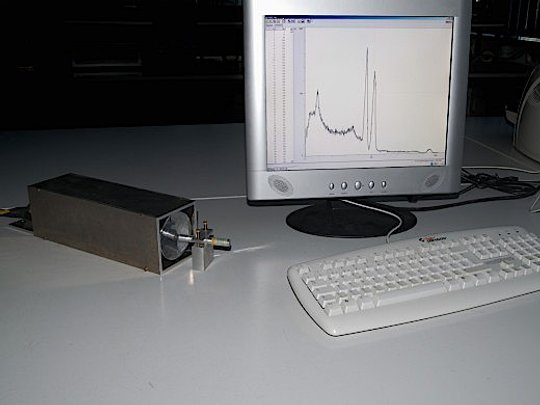 Abbildung 1: Überblick über den Versuchsaufbau; Kalibrierprobe vor dem Szintilationsdetektor (links) mit dem dazugehörigen Energiespektrum am Bildschirm.
Abbildung 1: Überblick über den Versuchsaufbau; Kalibrierprobe vor dem Szintilationsdetektor (links) mit dem dazugehörigen Energiespektrum am Bildschirm.
Versuch: Röntgenstrahlung (XST)
-
Kurzbeschreibung
-
Downloads
Anleitung RÖN -
Versuchsaufbau
 Abbildung 1: Überblick über den Versuchsaufbau
Abbildung 1: Überblick über den Versuchsaufbau
 Abbildung 2: Röntgenbild einer Tafel Vollnussschokolade
Abbildung 2: Röntgenbild einer Tafel Vollnussschokolade
 Abbildung 3: Röntgenbild einer Hand
Abbildung 3: Röntgenbild einer Hand
Versuch: Optische Abbildung (OPA)
-
Kurzbeschreibung
Im Versuch „Optische Abbildung” bestimmen Sie die Brennweite und die Hauptebenen eines Linsessystems mit verschiedenen Methoden (Autokollimation und Besselverfahren, Abbe-Verfahren). Ihre Messrrgebnisse vergleichen mit theoretischen Berechnungen und Simulationen.
-
Downloads
Anleitung OPA -
Versuchsaufbau
 Abbildung 1: Versuchsaufbau zur Autokollimation
Abbildung 1: Versuchsaufbau zur Autokollimation
 Abbildung 2: Versuchsaufbau zum Besselverfahren und zur Abbe-Methode
Abbildung 2: Versuchsaufbau zum Besselverfahren und zur Abbe-Methode
Versuch: Beugung und Brechung (BUB)
-
Kurzbeschreibung
-
Downloads
Anleitung BUB -
Versuchsaufbau
 Abbildung 1: Überblick über den Versuchsaufbau zur Brechung
Abbildung 1: Überblick über den Versuchsaufbau zur Brechung
 Abbildung 2: Die Spektrallinien der Hg-Spektraklampe durch das Prispenspektrometer betrachtet.
Abbildung 2: Die Spektrallinien der Hg-Spektraklampe durch das Prispenspektrometer betrachtet.
 Abbildung 3: Versuchsaufbau zur Beugung am Gitter.
Abbildung 3: Versuchsaufbau zur Beugung am Gitter.
Versuch: Stirlingmotor (STI)
-
Kurzbeschreibung
-
Downloads
Anleitung STI -
Versuchsaufbau
 Abb. 1: Versuchsaufbau
Abb. 1: Versuchsaufbau
Versuch: Interferometrie (INT)
-
Kurzbeschreibung
Im Versuch Interferometrie wird ein Michelson-Interferometer verwendet, um verschiedene Größen zu messen. Nach dem Einjustieren des Interferometers wird zunächst die Ganghöhe der Verstellschraube der Spiegelverstellung, indem die Zahl der auftretenden Interferenzmaxima (ider -minima) pro Schraubenumdrehung gemessen wird. Dann wird der Brechungsindex einer planparallelen Plexiglasscheibe über die Zal der Maxima beim Verdrehen der Scheibe bestimmt. Im letzten Versuchsteil wird der Brechungsindex von Luft bestimmt. Dazu wird eine Küvette in einen Arm des Interferometers gestellt, und die Zahl der Maxima beim Abpumpen der Küvette gezählt. -
Downloads
Anleitung INT -
Versuchsaufbau
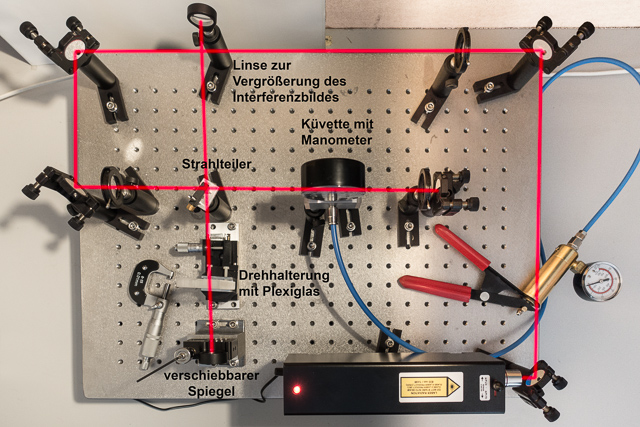 Abb. 1: Versuchsaufbau mit Strahlverlauf
Abb. 1: Versuchsaufbau mit Strahlverlauf
 Abb. 2: Interferenzmuster
Abb. 2: Interferenzmuster
 Abb. 3: Drehhalterung für Plexiglasplatte
Abb. 3: Drehhalterung für Plexiglasplatte -
Bestimmung des Gangunterschieds beim Durchgang durch die Plexiglasplatte
Abb. 4: Durchgang des Lichts durch den Plexiglasblock
Aus Abbildung 4 lässt sich der Gangunterschied zwischen dem geraden und dem um den Winkel α verdrehten Plexiglasblock folgendermaßen bestimmen:
Δs = 2·(n·AB' - n·AB - BC )
Der Faktor 2 rührt daher, dass die Interferometerarme zweimal durchlaufen werden. Weiterhin kann man schreiben:
AB = h
AB' = h / cos β
BC = AC - AB = AB' · cos(α-β ) - AB = h · cos(α-β ) / (cos β ) - h
sin β = sin α/n
cos β = (n² - sin²α)1/2 / n
cos(α-β ) = cos α · cos β + sin α · sin β
Insgesamt ergibt sich dann eine Abhängigkeit
Δs = N·λ = 2 · (1 - n - cos α +(n² - sin²α)1/2) · h
mit der Wellenlänge λ der gezählten Anzahl N der Interferenzstreifen, der Dicke h des Plexiglases und dem Brechungsindex n. Über eine Datenanpsssung (Fit) lässt sich dann der Brechungsindex bestimmen.
Betreuende
Blockpraktikum März 2022
- FHV: Lukas Spanier
- RAD: David Vogl
- XST:
- OPA: Robert Neagu
- BUB: Michael Mittermair
- INT: Jonathan Zerhoch
Sommersemester 2022
| Versuch | Betreuer | |
|---|---|---|
| Montag 14:15-17:15 | ||
| FHV | Ivana Pivarníková | |
| RAD | Marcel Lesch | |
| XST | Maximilian Horst | |
| OPA | Chiara Pinto / Luca Barioglio | |
| BUB | Ken Sachenbacher | |
| INT | Thien An Pham | |